Irregular Hexagon Area Calculator
Calculate the area of an irregular hexagon using coordinates (Shoelace / Gauss formula) or by entering side lengths and diagonals. Works for land, plots, roofs, and any 6-sided shape.
Coordinates
| # | X | Y |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Six-sided shapes show up in real life more often than we realize. A land boundary bends around a road. A roof footprint changes direction to fit the structure.
A floor plan grows unevenly as rooms are added over time. On paper, these shapes may still look like hexagons, but they no longer follow neat rules.
Once a hexagon loses equal sides and angles, simple formulas stop working. Guessing the area becomes risky, especially when the numbers matter.
That is where this Irregular Hexagon Area Calculator helps. It does not rely on assumptions. It works directly from coordinates, using a proven method trusted in real-world measurement.
What Is an Irregular Hexagon?
A hexagon is any shape with six sides.
It becomes irregular when:
- The sides are not the same length
- The angles are different
- The shape is not symmetrical
Most hexagons found in land, buildings, and layouts fall into this category. Once symmetry is gone, there is no shortcut formula that can calculate the area from side lengths alone.
Why Irregular Hexagons Are Difficult to Calculate
Irregular hexagons introduce more uncertainty than smaller shapes.
- There are many possible diagonals, each with a different length
- The shape may bend inward or outward
- Side measurements alone do not fully define the area
Breaking the shape into triangles often leads to different answers depending on how it is split. Coordinates solve this problem by fixing the exact position of every corner.
The Most Reliable Solution: Using Coordinates
This calculator uses the shoelace method, also known as the Gauss method.
You do not need to understand the formula to use it, but the idea is simple. The calculator takes the X and Y coordinates of each corner, in order around the shape, and calculates the area from those points.
This approach:
- Works for both convex and concave shapes
- Is not affected by orientation or rotation
- Produces exact results for straight-edged polygons
That is why coordinates are used in surveying, mapping software, CAD tools, and GIS systems.
How to Use the Irregular Hexagon Area Calculator
Using the calculator is straightforward.
- Choose your measurement unit
- Enter the X and Y coordinates for all six corners, in order
- Click calculate
The calculator processes the coordinates and displays the total area in square units. You do not need to handle formulas or conversions manually.
Where This Calculator Is Commonly Used
Land and Plot Measurement
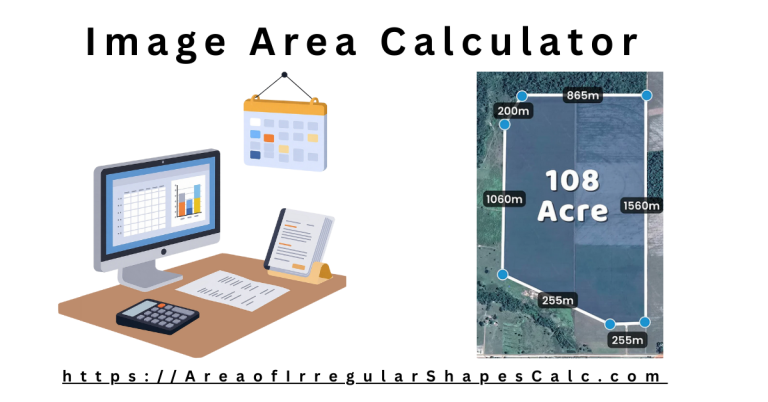
Property boundaries often curve around roads, rivers, or nearby plots, creating six-sided shapes that are far from regular. Using coordinates from survey data or maps gives an accurate and defensible area.
Roof Footprints and Structural Layouts
Roof designs frequently intersect at multiple angles, forming irregular hexagons. Accurate area calculation helps with material estimates and planning.
Floor Plans and Building Design
As buildings are expanded or renovated, floor layouts may evolve into six-sided shapes. Coordinates from drawings allow precise calculation of usable space.
Mapping and GIS Work
In mapping systems, regions are defined by points, not side lengths. This calculator follows the same logic, making it suitable for technical and professional workflows.
Engineering and Design Analysis
In constrained designs, boundaries often form irregular hexagons. Coordinate-based area calculation keeps results consistent across planning and execution.
Common Mistakes to Watch For
To get accurate results, avoid these issues:
- Entering points out of order
- Allowing edges to cross over each other
- Mixing coordinate units
- Assuming the shape is convex when it is not
Careful input prevents these problems and ensures reliable output.
When Should You Use This Calculator?
This calculator is the right choice when:
- The shape has exactly six sides
- You know the coordinates of each corner
- Accuracy is more important than approximation
If you only have side lengths, a pentagon or quadrilateral calculator may be more suitable. For freehand sketches, a draw or image-based tool works better.
Final Thoughts
Irregular hexagons reflect real-world constraints, not perfect geometry.
By describing the shape exactly as it exists, point by point, this calculator removes guesswork and delivers results you can trust. When precision matters, coordinates are the safest way to calculate area.